Structural design formulas for penstocks embedded in rock

The structural design formulas for penstocks embedded in rock which are shown in 'Technical standards for gates and penstock' in Japan are described.

Allowable stresss of steel material

$\begin{equation} \sigma_a = \min(\sigma_Y\: /\: SF_Y,\; \sigma_B\: /\: SF_B) \end{equation}$

$\begin{align} &\sigma_a & &\text{allowable stress of steel plate}\\ &\sigma_Y & &\text{yield strength of steel plate}\\ &\sigma_B & &\text{tensile strehgth of steel plate}\\ &SF_Y & &\text{safety factor for yield strength (= 1.80)}\\ &SF_B & &\text{safety factor for tensile strength (= 2.35)} \end{align}$

Welded joint efficiency

Location of welding	RT or UT carrying out for more than 5% of welded joint length	RT or UT carrying out for less than 5% of welded joint length
Factory welding	95%	85%
Site welding	90%	80%

Required safety factor for buckling due to external pressure

Pipe shell

$\begin{equation} \cfrac{p_k}{P_o} \geq 1.5 \end{equation}$

$\begin{align} &p_k & &\text{critical buckling pressure of steel pipe}\\ &P_o & &\text{external pressure}\\ \end{align}$

Stiffener

$\begin{equation} \cfrac{\sigma_{cr}}{\sigma_c} \geq 1.5 \end{equation}$

$\begin{align} &\sigma_{cr} & &\text{critical buckling stress of stiffener}\\ &\sigma_c & &\text{average compressive stress of stiffener}\\ \end{align}$

Design internal pressure

f:id:damyarou:20200625160211j:plain

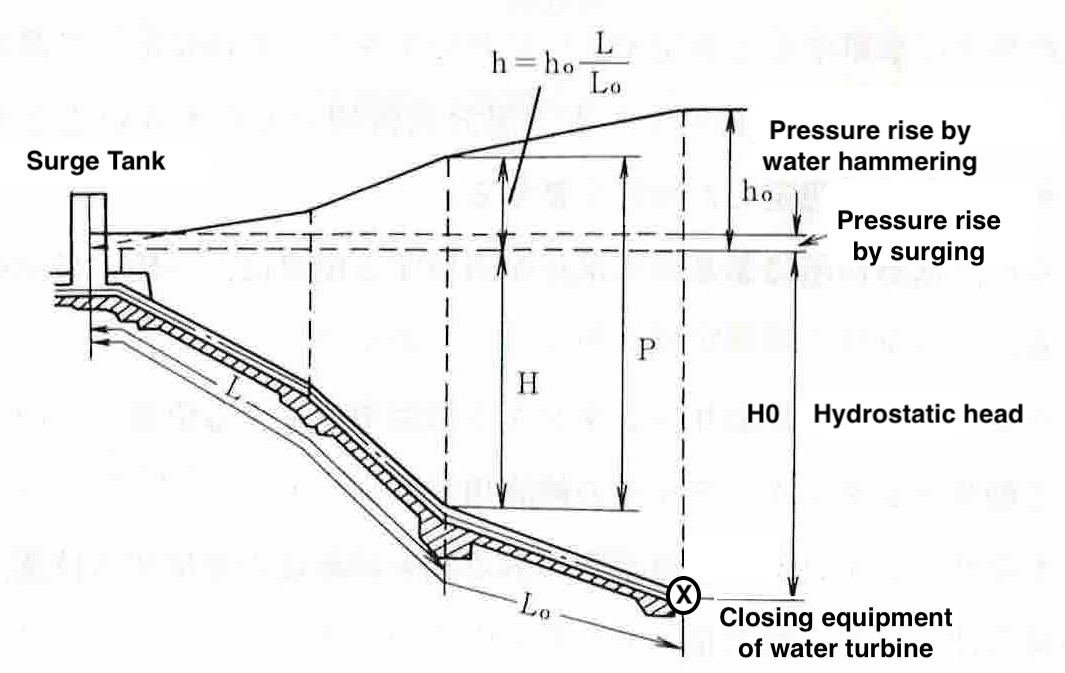
Definition of dimensions

f:id:damyarou:20200625160239j:plain

$\begin{align} &D_0 & &\text{design internal diameter}\\ &D_0' & &\text{design external diameter}\\ &D & &\text{internal diameter adding 1/2 the corrosion allowance}\\ & & &\text{from the internal surface of the pipe shell ($D=D_0 + \epsilon$})\\ &D' & &\text{external diameter subtracting 1/2 the corrosion allowance}\\ & & &\text{from the external surface of the pipe shell ($D'=D_0' - \epsilon$)}\\ &D_m & &\text{diameter of the center of plate thickness ($D_m=2 r_m$)}\\ &r_m & &\text{radius of the center of plate thickness $(r_m=(D_0 + t_0)\:/\:2$)}\\ &t_0 & &\text{design shell thickness}\\ &t & &\text{shell thickness excluding corrosion allowance ($t=t_0 - \epsilon$)}\\ &\epsilon & &\text{allowance thickness for corrosion and wear}\\ \end{align}$

Corrosion allowance

An allowance of more than or equal to 1.5mm shall be provided against corrossion and wear.

Minimum shell thickness

The minimum shell thickness used for the pressure lining part shall be more than or equal to those determined from following formula, if stiffeners are not used.

$\begin{equation} t_0=\cfrac{D_0 + 800}{400} \end{equation}$

The minimum shell thickness shall not be less than 6mm even if the pipe diameter is small and stiffeners are used.

Stress calculation

Tensile stress in circumferential direction due to internal pressure

General

$\begin{equation} \sigma=\cfrac{P\cdot D}{2\cdot t} \quad \text{or} \quad \sigma=\cfrac{P\cdot D}{2\cdot (t_0 - \epsilon)} \end{equation}$

Internal pressure shared design by bedrock

$\begin{equation} \sigma=\cfrac{P\cdot D}{2\cdot t}\cdot (1-\lambda) \end{equation}$

$\begin{equation} \lambda=\cfrac{1-\cfrac{E_s}{P}\cdot \alpha_s\cdot \Delta T\cdot \cfrac{2\cdot t}{D}} {1+(1+\beta_c)\cdot \cfrac{E_s}{E_c}\cdot \cfrac{2\cdot t}{D}\cdot \log_e\cfrac{D_R}{D} +(1+\beta_g)\cdot \cfrac{E_s}{E_g}\cdot \cfrac{m_g+1}{m_g}\cdot \cfrac{2\cdot t}{D}} \end{equation}$

$\begin{align} &\sigma & & \text{tensile stress in circumferential direction of pipe}\\ &P & & \text{internal pressure}\\ &\lambda & & \text{sharing ratio of internal pressure by bedrock}\\ &E_s & & \text{elastic modulus of steel}\\ &\alpha_s & & \text{coefficient of linear expansion of steel}\\ &\Delta T & & \text{temperature change of steel penstock}\\ &\beta_c & & \text{coefficient of plastic deformation of concrete}\\ &E_c & & \text{elastic modulus of concrete}\\ &D_R & & \text{excavation diameter of tunnel}\\ &\beta_g & & \text{coefficient of plastic deformation of bedrock}\\ &E_g & & \text{elastic modulus of bedrock}\\ &m_g & & \text{Poisson's number of bedrock} \end{align}$

$\begin{equation} t=\cfrac{P\cdot D}{2\cdot \eta\cdot \sigma_a} -\cfrac{\eta\cdot \sigma_a-E_s\cdot \alpha_s\cdot \Delta T} {\eta\cdot \sigma_a\cdot \left\{(1+\beta_c)\cdot \cfrac{E_s}{E_c}\cdot \cfrac{2}{D}\cdot \log_e\cfrac{D_R}{D} +(1+\beta_g)\cdot \cfrac{E_s}{E_g}\cdot \cfrac{m_g+1}{m_g}\cdot \cfrac{2}{D}\right\}} \end{equation}$

$\begin{align} &\sigma_a & &\text{allowable stress of steel}\\ &\eta & &\text{welded joint efficiency} \end{align}$

Tensile stress in penstock axis direction

Stress due to restraint by stiffener

$\begin{equation} \sigma=1.82\cdot \cfrac{t_r\cdot h_r}{A_r}\cdot \cfrac{P\cdot D}{2\cdot t}\cdot (1-\lambda) \end{equation}$

$\begin{equation} A_r=t_r\cdot h_r+\left(1.56\cdot \sqrt{r_m\cdot t}+t_r\right)\cdot t \end{equation}$

f:id:damyarou:20200625160336j:plain

Stress due to temperature change

$\begin{equation} \sigma=\alpha_s\cdot E_s\cdot \Delta T \end{equation}$

$\begin{align} &\sigma & & \text{stress due to temperature change}\\ &\alpha_s & & \text{coefficient of linear expansion of steel}\\ &E_s & & \text{elastic modulus of steel}\\ &\Delta T & & \text{temperature change} \end{align}$

Stress due to Poisson's effect

$\begin{equation} \sigma=\nu_s\cdot \sigma_r \end{equation}$

$\begin{align} &\sigma & & \text{stress due to Poisson's effect}\\ &\nu_s & & \text{Poisson's ratio of steel}\\ &\sigma_r & & \text{circumferential stress} \end{align}$

Calculation for external presure

Without stiffener (E. Amstutz's formula)

$\begin{equation} p_k=\cfrac{\sigma_N}{\cfrac{r_m}{t}\left(1+0.35\cdot \cfrac{r_m}{t}\cdot \cfrac{\sigma_F^*-\sigma_N}{E_s^*}\right)} \qquad 35 < \cfrac{r_m}{t} \end{equation}$

$\begin{equation} \left(\cfrac{k_0}{r_m}+\cfrac{\sigma_N}{E_s^*}\right) \cdot \left(1+12\cdot \cfrac{r_m^2}{t^2}\cdot \cfrac{\sigma_N}{E_s^*}\right)^{1.5} =3.36\cdot \cfrac{r_m}{t}\cdot \cfrac{\sigma_F^*-\sigma_N}{E_s^*} \cdot \left(1-\cfrac{1}{2}\cdot \cfrac{r_m}{t}\cdot \cfrac{\sigma_F^*-\sigma_N}{E_s^*}\right) \end{equation}$

$\begin{equation} k_0=\cfrac{\left(\alpha_s\cdot \Delta T+\beta_g\cdot \cfrac{\sigma_a\cdot \eta}{E_s}\right)\cdot r_0'}{1+\beta_g} \quad \text{or} \quad k_0=0.4\times 10^{-3}\cdot r_m \end{equation}$

$\begin{equation} E_s^*=\cfrac{E_s}{1-\nu_s{}^2} \end{equation}$

$\begin{equation} \sigma_F^*=\mu\cdot \cfrac{\sigma_F}{\sqrt{1-\nu_s+\nu_s{}^2}} \qquad \mu=1.5-0.5\cdot \cfrac{1}{\left(1+0.002\cdot \cfrac{E_s}{\sigma_F}\right)^2} \end{equation}$

$\begin{align} &p_k & &\text{critical buckling pressure of pipe shell without stiffener}\\ &k_0 & &\text{gap between concrete and external surface of pipe}\\ &\sigma_a & &\text{allowable stress of steel}\\ &\eta & &\text{welded joint efficiency}\\ &\sigma_N & &\text{circumferential direct stress at deformed pipe shell portion}\\ &\sigma_F & &\text{yield point of steel}\\ &E_s & &\text{elastic modulus of steel}\\ &\nu_s & &\text{Poisson's ratio of steel} \end{align}$

With stiffener

Pipe shell proper (S. Timoshenko's formula)

$\begin{equation} \cfrac{(1-\nu_s{}^2)\cdot r_0'\cdot p_k}{E_s\cdot t} =\cfrac{1-\nu_s{}^2}{(n^2-1)\cdot \left(1+\cfrac{n^2\cdot l^2}{\pi^2\cdot r_0'{}^2}\right)^2} +\cfrac{l^2}{12\cdot r_0'{}^2}\cdot \left\{(n^2-1)+\cfrac{2\cdot n^2-1-\nu_s}{1+\cfrac{n^2\cdot l^2}{\pi^2\cdot r_0'{}^2}}\right\} \end{equation}$

$\begin{align} &p_k & &\text{critical buckling pressure of pipe shell with stiffener}\\ &n & &\text{number of wrinkles}\\ &l & &\text{actual interval of stiffeners} \end{align}$

$\begin{equation} l'=\left(l+1.56\cdot \sqrt{r_m\cdot t}\cdot \cos^{-1}\lambda\right)\cdot \left(1+0.037\cdot \cfrac{\sqrt{r_m\cdot t}}{l+1.56\cdot \sqrt{r_m\cdot t}\cdot \cos^{-1}\lambda} \cdot \cfrac{t^3}{I_s} \right) \end{equation}$

$\begin{equation} \lambda=1-(1+T)\cdot \cfrac{1+\cfrac{t_r}{1.56\cdot \sqrt{r_m\cdot t}}}{1+\cfrac{S_0}{1.56\cdot \sqrt{r_m\cdot t}}} \end{equation}$

$\begin{equation} T=\cfrac{2\cdot C}{t_r+1.56\cdot \sqrt{r_m\cdot t}} \end{equation}$

$\begin{equation} C=\cfrac{\cfrac{r_0'{}^2}{t}-\cfrac{(t_r+1.56\cdot \sqrt{r_m\cdot t})\cdot r_0'{}^2}{S_0+1.56\cdot t\cdot \sqrt{r_m\cdot t}}} {\cfrac{3}{\{3\cdot (1-\nu_s{}^2)\}^{0.75}}\cdot \left(\cfrac{r_0'}{t}\right)^{1.5}\cdot \cfrac{\sinh(\beta\cdot l)+\sin(\beta\cdot l)}{\cosh(\beta\cdot l)-\cos(\beta\cdot l)} +\cfrac{2\cdot r_0'{}^2}{S_0+1.56\cdot t\cdot \sqrt{r_m\cdot t}} } \end{equation}$

$\begin{equation} \beta=\cfrac{\{3\cdot (1-\nu_s{}^2)\}^{0.25}}{\sqrt{r_m\cdot t}} \end{equation}$

$\begin{equation} S_0=t_r\cdot (t+h_r) \qquad I_s=\cfrac{t_r}{12}\cdot (t+h_r)^3 \end{equation}$

$\begin{align} &l' & &\text{modified interval of stiffeners by Nagashima and Kozuki}\\ &S_0 & &\text{section area of stiffener}\\ &I_s & &\text{moment of inertia of stiffener} \end{align}$

f:id:damyarou:20200625160458j:plain

Stiffener (E. Amstutz's formula)

$\begin{equation} \sigma_{cr}=\sigma_N\cdot \left\{1-\cfrac{r_0'}{e}\cdot \cfrac{\sigma_F-\sigma_N} {\left(1+\cfrac{3}{2}\cdot \pi\right)\cdot E_s}\right\} \end{equation}$

$\begin{equation} \left(\cfrac{k_0}{r_m}+\cfrac{\sigma_N}{E_s}\right)\cdot \left(1+\cfrac{r_m{}^2}{i^2}\cdot \cfrac{\sigma_N}{E_s}\right)^{1.5} =1.68\cdot \cfrac{r_m}{e}\cdot \cfrac{\sigma_F-\sigma_N}{E_s}\cdot \left(1-\cfrac{1}{4}\cdot \cfrac{r_m}{e}\cdot \cfrac{\sigma_F-\sigma_N}{E_s}\right) \end{equation}$

$\begin{align} &\sigma_{cr} & &\text{critical buckling stress of stiffener}\\ &i & &\text{radius of gyration of combined section of stiffeners}\\ &e & &\text{distance from the center of gravity of a combined section}\\ & & &\text{of stiffener to internal surface of the pipe} \end{align}$

$\begin{equation} \sigma_c=\cfrac{p'\cdot r_0'\cdot (t_r+1.56\cdot \sqrt{r_m\cdot t})} {S_0+1.56\cdot t\cdot \sqrt{r_m\cdot t}} \end{equation}$

$\begin{equation} p'=\cfrac{p}{t_r+1.56\cdot \sqrt{r_m\cdot t}}\cdot \left\{(t_r+1.56\cdot \sqrt{r_m\cdot t})+2\cdot C\right\} \end{equation}$

$\begin{align} &\sigma_c & &\text{average compressive stress of stiffener}\\ &p & &\text{external pressure}\\ &p' & &\text{modified external pressure summing up shearing force}\\ & & &\text{acting both sides of a stiffener from a pipe shell}\\ &C & &\text{coefficient defined in Nagashima and Kozuki's formula} \end{align}$

$\begin{equation} S_f=\cfrac{\sigma_{cr}}{\sigma_c} \qquad \text{(safety factor of stiffener)} \end{equation}$

f:id:damyarou:20200625160527j:plain

That's all.